(!)亲爱的顾客,您所使用的IE浏览器,微软公司已不再提供技术支持,为避免可能产生的米思米网站浏览体验影响,建议您使用Windows10系统及最新的谷歌Chrome或微软Edge浏览器访问本网站。 若您使用360浏览器的兼容模式,请切换到极速模式继续访问。也可以通过应用市场下载米思米闪购商城APP进行访问,谢谢。
- 米思米MISUMI首页
- > 技术之窗
- > 技术信息
- > 〔技术计算〕线性系统的寿命计算2
〔技术计算〕线性系统的寿命计算 2
|
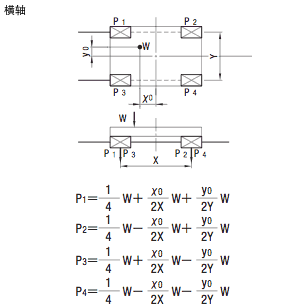
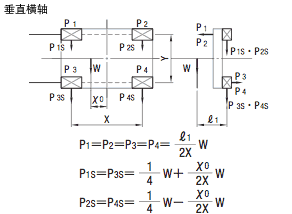
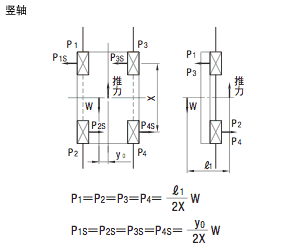
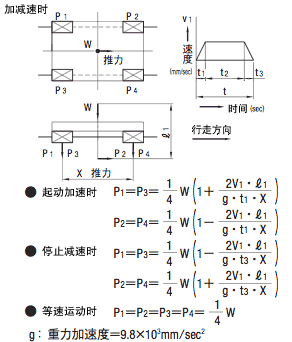
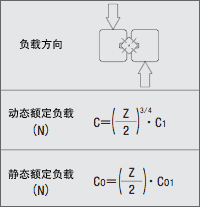
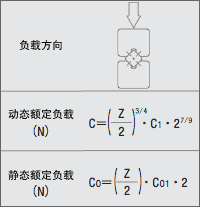
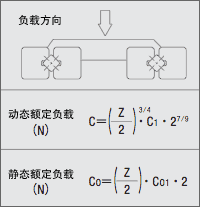
●负载计算
X、Y: 线性系统的跨距(mm) V:移动速度(mm/sec) t1 : 加速时间(sec) t3 : 减速时间(sec) 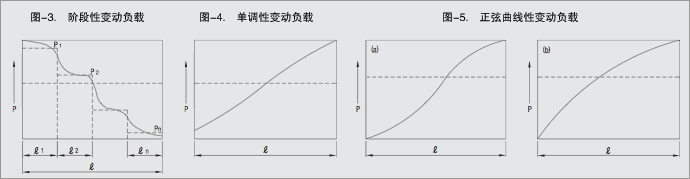 |
|
●●变动负载的等效负载
直线导轨额定寿命是指在相同条件下,分别使一群相同的直线导轨行走时,其中90%不发生剥落而达到的总行走距离。
|